রেজিস্টার (Resister) একগুচ্ছ ফিল্প-ফ্লপের সাহায্যে গঠিত ক্ষুদ্র অস্থায়ী মেমোরি ডিভাইসকে Resister বলে। রেজিস্টারে ব্যবহৃত প্রতিটি ফিল্প-ফ্লপ একটি করে বাইনারি বিট
তৃতীয় অধ্যায় লেকচার-১৬: রেজিস্টার এবং কাউন্টার সম্পর্কে আলোচনা।
Category: Chapter-3
তৃতীয় অধ্যায় লেকচার-১৫: অ্যাডার (Adder) বা যোগের বর্তনী।
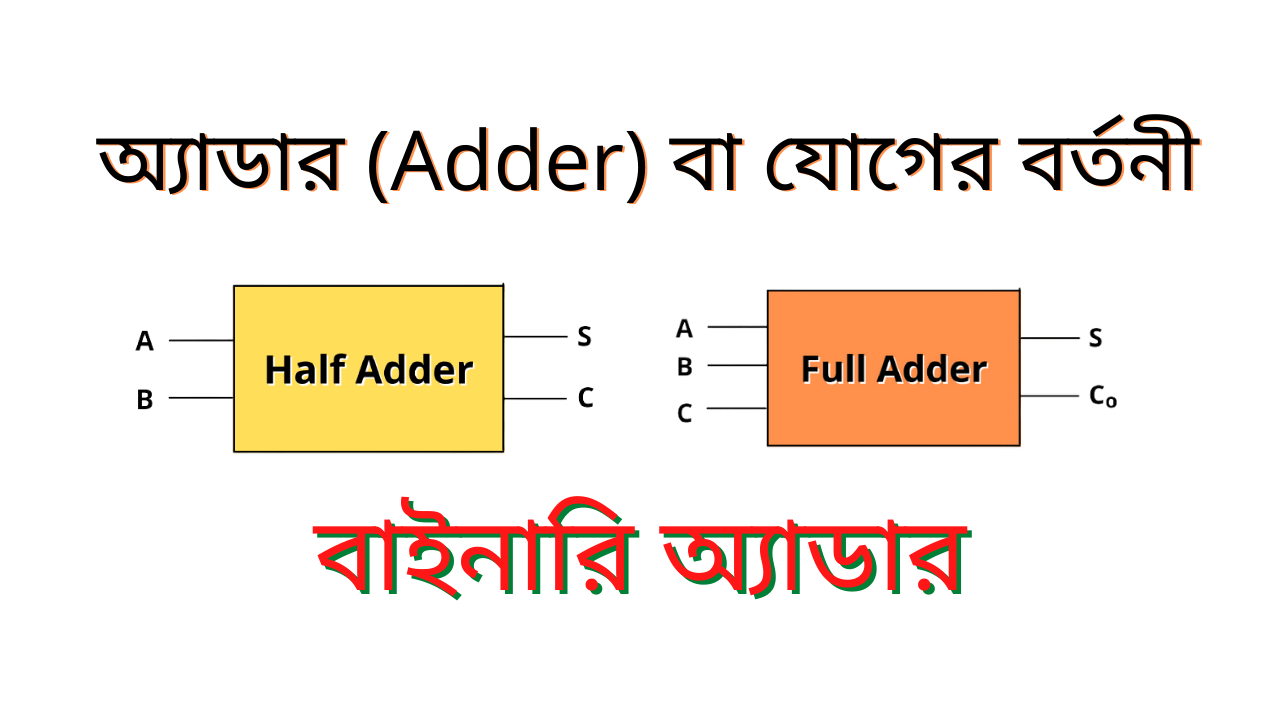
অ্যাডার(Adder) যে সার্কিট বাইনারি বিটকে যোগ করে তাকে অ্যাডার বলে। অথবা, যে সার্কিট যোগের কাজ সম্পন্ন করে তাকে Adder বলে।
তৃতীয় অধ্যায় লেকচার-১৪: এনকোডার এবং ডিকোডার এর আলোচনা।
এনকোডার (Encoder) যে ডিজিটাল বর্তনী মানুষের ভাষাকে কম্পিউটারের বোধগম্য ভাষায় রুপান্তর করে তাকে Encoder বলে। এটি আনকোডেড ডেটাকে কোডেড ডেটায়
তৃতীয় অধ্যায় লেকচার-১৩: সার্বজনীন গেটের (NAND & NOR) প্রমাণ।
সার্বজনীন গেইট যে গেইট দ্বারা মৌলিক গেটসহ (OR, AND, NOT) যে কোন গেইট এবং যে কোন সার্কিট বাস্তবায়ন করা যায়
তৃতীয় অধ্যায় লেকচার-১২: লজিক ফাংশন থেকে লজিক সার্কিটে রুপান্তর এবং সার্কিট থেকে ফাংশন নির্ণয়।
Logic Function থেকে Logic Circuit এ রুপান্তর লজিক ফাংশন বা সমীকরণ থেকে Logic Circuit এ রুপান্তর করতে হলে যে নিয়মগুলি
তৃতীয় অধ্যায় লেকচার-১১: যৌগিক গেটসমূহের(NAND, NOR, X-OR, X-NOR) বর্ণনা।
যৌগিক গেইট : দুই বা ততোধিক মৌলিক গেইটের সাহায্যে যে গেইট তৈরি হয় তাকে যৌগিক গেইট বলে। যৌগিক গেইট মৌলিক
তৃতীয় অধ্যায় লেকচার-০৭: সত্যক সারণী তৈরি এবং সারণী থেকে সমীকরণ নির্ণয়।
সত্যক সারণী (Truth Table) যে সারণীর মাধ্যমে বুলিয়ান বীজগাণিতের বিভিন্ন ইনপুটের মানগুলোর সম্ভাব্য আউটপুট মান দেখানো যায় তাকে সত্যক সারণী
তৃতীয় অধ্যায় লেকচার-০৮: ডি-মরগ্যানের উপপাদ্য (De Morgan’s Theorem)।
ডি-মরগ্যানের উপপাদ্য ইংরেজ গণিতবিদ ডি-মরগ্যান (De Morgan) বুলিয়ান অ্যালজেবরার ক্ষেত্রে দুটি উপপাদ্য আবিষ্কার করেন, তার নাম অনুসারে উপপাদ্য দুটিকে ডি-মরগ্যানের
তৃতীয় অধ্যায় লেকচার-০৬: বুলিয়ান অ্যালজেবরা ও বুলিয়ান উপপাদ্য।
বুলিয়ান অ্যালজেবরা ⇒ ব্রিটিশ গণিতবিধ ও দার্শনিক জর্জ বুল ১৮৪৭ সালে তার প্রকাশিত প্রথম গ্রন্থ “The Mathematical Analysis of Logic”
তৃতীয় অধ্যায় লেকচার-০৫: কোড (Code-BCD, ASCII, EBCDIC, Unicode)
কোডের পরিচিতি: কম্পিউটার সিস্টেমে ব্যবহৃত প্রতিটি বর্ণ, অংক, গাণিতিক চিহ্ন ও বিশেষ চিহ্নসমূহকে পৃথক পৃথকভাবে সিপিইউকে বোঝানোর জন্য যে অদ্বিতীয়
তৃতীয় অধ্যায় লেকচার-০৪: পরিপূরক (Complement) নির্নয়।
পরিপূরক এর আলোচনা : চিহ্নযুক্ত সংখ্যা: পরিপূরক জানার পূর্বে চিহ্নযুক্ত সংখ্যা সম্বন্ধে জানতে হবে। চিহ্নযুক্ত সংখ্যা হলো যখন কোন সংখ্যার
তৃতীয় অধ্যায় লেকচার-০৩: বিভিন্ন সংখ্যা পদ্ধতির মধ্যে যোগ ও বিয়োগ।
দশমিক(ডেসিমাল) সংখ্যার যোগ: ধাপ-০১: দশমিক সংখ্যায় একাধিক অংকের যোগফল ভিত্তি ১০ এর সমান বা বেশি হলে যোগফল থেকে ভিত্তি ১০
তৃতীয় অধ্যায় লেকচার-০২: সংখ্যা পদ্ধতির রুপান্তর(Conversion of Number System)
সংখ্যা পদ্ধতির রুপান্তর(Conversion of Number System) এক সংখ্যা পদ্ধতি থেকে অন্য সংখ্যা পদ্ধতিতে পরিবর্তন করাকে সংখ্যা পদ্ধতির রুপান্তর বলে। আমরা
তৃতীয় অধ্যায় লেকচার-০১:সংখ্যা পদ্ধতি ও এর প্রকারভেদ।
সংখ্যা পদ্ধতি(Number System) বিভিন্ন সাংকেতিক চিহ্ন বা অঙ্ক(ডিজিট) ব্যবহার করে সংখ্যা লেখা ও প্রকাশ করার পদ্ধতিতে সংখ্যা পদ্ধতি বা Number
